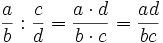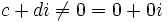Делимое как его приготовить

Картофель крупный 4 шт.Сыр тертый 150 г Масло сливочное 50 гБекон 100 гСоль, перец по вкусуСпособ приготовления: Картофель тщательно вымыть, подсушить и выложить на противень.Запекать картофель в предварительно разогретой до 200С духовке около 40.

Кальмары 4 тушкиАнчоусы (в масле) 6 шт. Апельсин 1 шт.Каперсы 1-2 горстиПетрушка средний пучокЧеснок 2 зубчикаПанировочные сухари 1/2 ст.Масло оливковое 2 ст. л.Соль, перец по вкусуСпособ приготовления: Чеснок очистить и мелко нарезать. Петрушку мелко.

Нам понадобится обычная пластиковая бутылка на 1,5 литра и воронка. Насыпаем/наливаем в бутылку: 10 ст.ложек (с горкой) муки, 2 яйца, 3 ст.ложки сахара, пол чайной ложки соли, 3 ст.ложки растительного масла и 600 г.

Ингредиенты сыр моцарелла — 150 г помидоры черри — 150 г листья зеленого салата — 30 г зеленые оливки без косточки — 70 г кедровые орехи — 50 г оливковое масло — 0,5 ст.

Ингредиенты: — 5-7 шт картофеля среднего размера — 2 яичных белка — паприка — соль по-вкусу Приготовление: 1. Многие из нас любят картофель “Фри”, но все прекрасно знают, что он не полезен для здоровья.

1 Комментарий

Большое спасибо за рецепты новые, с удовольствием буду экспериментировать. Мне тоже очень нравятся сыры с сучужным именно, сейчас покупаю Бакздрав. Пробовала микробиальный и чистый пепсин искусственный, совсем не то. На сычуге и горечи нет, и выход максимальный.

Источник

Делимое

Деле́ние (операция деления) — это одно из четырёх простейших арифметических действий, обратное умножению.

Подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание.

Рассмотрим, например, такой вопрос:

сколько раз 3 содержится в 14?

Повторяя операцию вычитания 3 из 14, мы находим, что 3 «входит» в 14 четыре раза, и еще «остаётся» число 2

Результат деления также называют отношением.

Содержание

Деление натуральных чисел

Деление не замкнуто в кольце целых чисел. Простым языком это означает то, что деление одного целого числа на другое может не быть целым. В случае, если всё-таки результат является целым числом, говорят о делении без остатка.

Деление чисел издавна считалось самой трудной из арифметических операций. Было время, когда «секрет» деления знало не очень много посвящённых людей, и буквально передавало из поколения в поколение. Происходило это потому, что существовавшие алгоритмы деления были очень громоздки, сложны для исполнения и запоминания (например, деление в виде корабля). Появление деления столбиком радикально изменило эту ситуацию — теперь деление входит в раннюю школьную программу по математике наряду с остальными арифметическими действиями. Однако так же, как и в случае с умножением, в последнее время открыты более эффективные алгоритмы (см. en:Division (digital), применяющиеся в вычислительной технике.

Существуют правила, позволяющие быстро определить, делится ли число на заданный делитель без остатка (признаки делимости). Наиболее известные признаки делимости на 2, 3, 4, 5, 8, 9, 11, 25 и их производные, также существует признаки делимости на 7, 13, 1001 и другие числа.

Целое число, на которое одновременно делятся без остатка несколько чисел, называется их общим делителем.

Определение количества делителей натурального числа приводит к двум важным понятиям: составное и простое число. У простого числа есть только два делителя — 1 и само число.

В случае, если одно натуральное число не делится на другое без остатка, можно говорить о делении с остатком. Рассмотрение остатков, их сравнение и формализация в виде вычетов привели к целой науке — теории чисел.

Обычно на остаток накладываются следующие ограничения (чтобы он был корректно, т.е. однозначно, определён):

. .

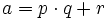
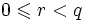
Где a — делимое, p — делитель, q — частное и r — остаток.

Деление целых чисел

Деление произвольных целых чисел не существенно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.

Однако деление целых чисел с остатком определяется по-разному. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, − 7 / ( − 3) = 2 с остатком (-1)); в другом случае понятие остатка напрямую обобщается и ограничения заимствуются из натуральных чисел:

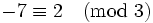
Деление рациональных чисел

Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).

Правило деления обыкновенных дробей:

Деление вещественных чисел

Деление также замкнуто в поле ненулевых вещественных чисел. Сечение Дедекинда позволяет однозначно определить результат деления.

Деление комплексных чисел

Комплексные числа опять замкнуты относительно операции деления.

В алгебраическое форме результат можно получить путём домножения на сопряжённое число:

. Результат определён для всех

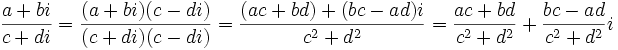
В экспоненциальной форме легче всего получить результат:

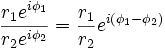
. Видно, что при этом модули делятся, а аргументы вычитаются.

Аналогично в тригонометрической форме:

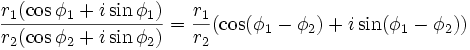
Деление в алгебре

В отличие от простейших арифметических случаев на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.

Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым ( x − 1 * x = e ), так и правым ( x * x − 1 = e ). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

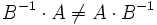
Отношение тензоров в общем случае не определено.

Деление многочленов

В общих чертах оно повторяет идеи деления натуральных чисел, ибо натуральное число есть ничто иное как значения многочлена, у которого коэффициенты — цифры, а вместо переменной стоит основание системы счисления:

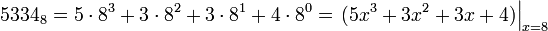
Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.

Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.

Деление на ноль

По правилам арифметики деление на число 0 запрещено, поскольку оно приводит к противоречию. Другое дело — деление на бесконечно малую функцию или последовательность (которые можно считать «нулями» в соответствующих множествах). Деление конечных функций на бесконечно малые приводит к появлению бесконечно больших, а отношение двух бесконечно малых называется неопределённостью 0/0, которую можно преобразовать (см. раскрытие неопределённостей) с тем, чтобы получить определённый результат.

Источник

Общее представление о делении натуральных чисел

В рамках этого материала мы разберем важное действие, называемое делением. Дав общее представление о нем и объяснив его смысл, мы введем основные термины и обозначения на письме. В последнем пункте мы расскажем, для решения каких задач нам пригодится умение делить натуральные числа.

Что такое деление натуральных чисел

Само по себе понятие деление неразрывно связано с процессом разъединения некоторого множества предметов на несколько отдельных множеств.

Объясним на примере.

В быту мы часто употребляем слова»делиться», «поделиться», например, поделиться угощением с друзьями. Это слово означает, что угощение мы поделили на некоторые части и отдали часть одним людям, а часть другим (или оставили себе). С помощью этого простого примера деление можно представить как последовательное вычитание из одного большого множества. Что такое вычитание и как его выполнять, мы уже разбирали с вами ранее.

Проще всего понять процесс деления на равные части. У нас есть исходное множество, которое возможно разделить на некоторое количество одинаковых множеств. Например, мы разделили конфеты между друзьями так, что у каждого стало, например, по 5 . Тогда мы можем сказать, что поделили угощение поровну. В этом смысле деление обратно умножению (см. понятие об умножении натуральных чисел). Далее по ходу статьи мы будем разбирать только деление на равные части. Делению с остатком посвящен отдельный материал.

Основной смысл процесса деления

На основе того, что мы озвучили, можно придать определенный смысл делению одного натурального числа на другое (отдельно выделим число, которое делят, и то, на которое делят). Мы помним, что понятие натуральных чисел проще всего соотнести с количеством некоторых предметов. То число, которое необходимо поделить, выражает число предметов исходного множества. В зависимости от того, какой смысл мы придаем второму числу (т.е. тому, на которое делят), можно выделить два основных подхода к пониманию смысла деления. Возможны такие варианты:

1. Исходное число, на которое осуществляется деление, соотносится с количеством предметов в тех множествах, что мы получили в результате деления. Тогда полученное после деления число будет означать количество получившихся множеств. Например, мы разделили 10 конфет на кучки по 2 штуки в каждой. Поделив 10 на 2 , мы узнаем число кучек.

2. Исходное число, на которое мы делим, соответствует количеству получившихся множеств. Тогда результат деления будет показывать нам, сколько элементов входит в каждое такое множество. Вернувшись к примеру выше, мы увидим, что если 10 конфет разложить на 5 кучек, то число 2 , получившееся в итоге, соответствует количеству конфет в каждой кучке.

Разделить одно натуральное число на другое без остатка возможно далеко не всегда. Так, 10 конфет мы можем ровно разделить на 2 или 5 кучек, а на 3 нет, потому что в одном из множеств окажется отличное от других число конфет. Разложить 10 конфет по 15 или 20 кучкам мы также не в состоянии. Смысл таких действий объясняется в материале про деление с остатком.

Если мы можем поделить одно натуральное число на другое, то получившееся в итоге число также будет натуральным.

Основные понятия процесса деления

В этом пункте мы укажем основные обозначения и понятия, используемые в делении натуральных чисел.

Чтобы обозначить деление в записи, обычно используют знак двоеточия: « : ». Иногда можно встретить вместо него знак « ÷ », который означает то же самое. Первым мы записываем число, которое будем делить, потом знак деления, а потом число, на которое делим. Числовое выражение вида 10 : 5 означает, что мы делим десять на пять.

То число, которое делим, называем делимым. То, на которое делим – делителем. Итог вычислений правильно называть частным. Само числовое выражение, состоящее из делимого, делителя и знака деления, тоже называется частным.

В примере 30 : 6 натуральное число 30 – это делимое, 6 – делитель, а 5 , получившаяся в итоге, – частным.

Когда мы говорим о том, что нужно определить число, являющееся результатом деления одного натурального числа на другое, нужно использовать выражения «найти частное» или «вычислить частное».

Все вместе – делимое, делитель и частное со знаками деления и равенства – обычно записывается в виде равенства. Например, 5 является частным от деления 30 на 6 . Мы можем записать это так:

Запись читается как «тридцать разделить на шесть равно пяти» или «частное от деления тридцати на шесть равно пяти».

Схематично процесс деления можно отобразить как » делимое : делитель = частное.».

Задачи с применением деления

Приведем примеры задач, для которых нужно уметь делить одно натуральное число на другое.

1. Первый тип задач – это те, в которых нужно найти, сколько множеств получится после деления исходного множества на равные части, а также близкие к ним задачи на вычисление количества предметов в каждом множестве после деления. Ранее мы уже приводили примеры таких задач. Добавим еще несколько.

Допустим, у нас есть 40 ручек, которые нужно распределить поровну между 4 коробками. Как вычислить, сколько ручек положить в каждую из них?

Разделить 40 на 4 .

Ответ: 10

На ужин было приготовлено 12 котлет. Каждому члену семьи должно достаться по две. Сколько всего человек будут ужинать?

Разделим 12 на 2 .

Ответ: 6 .

2. Второй тип задач очень схож с первым, однако в них необходимо вычислить не количество предметов, а изменения физических величин (времени, температуры, длины и др.)

Например, у нас есть полная бочка молока объемом 100 л. Сколько надо взять двухлитровых бутылок, чтобы перелить туда все имеющееся молоко?

Для решения задачи нам надо разделить 200 на 2 .

Ответ: 100

30 -метровый шнур надо разрезать на 10 равных частей. Какой длины будет каждая из них?

Здесь опять же нам надо вычислить частное 30 : 10 .

Ответ: 3

3. Третий тип задач – это те, где нужно найти, во сколько раз уменьшилось исходное количество чего-либо, или выяснить, во сколько одно множество предметов или величина больше, чем другое. Например:

Планировалось построить дом площадью 120 кв м., но в итоге построили в два раза меньше. Какую площадь имеет в итоге построенный дом?

Для решения этой задачи нам нужно разделить 120 : 2 .

Ответ: 60

С одной яблони мы собрали 60 яблок, а с другой – в три раза меньше. Сколько яблок сорвали со второй яблони? Чтобы дать ответ на это вопрос, требуется разделить 60 на 3 .

Источник