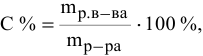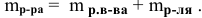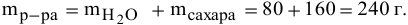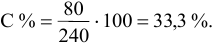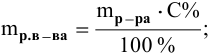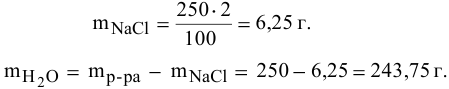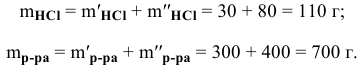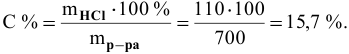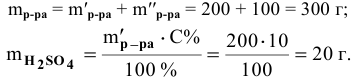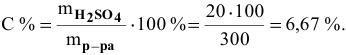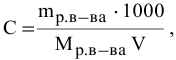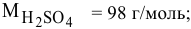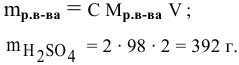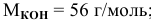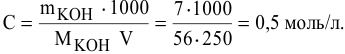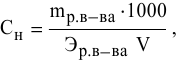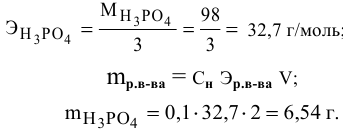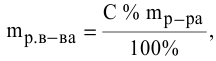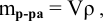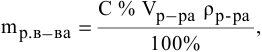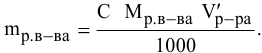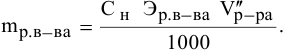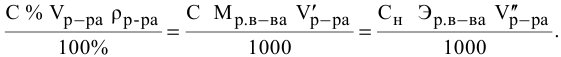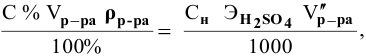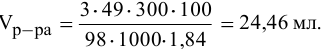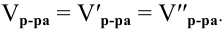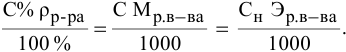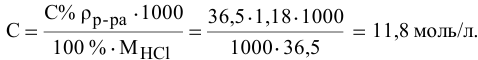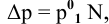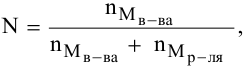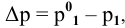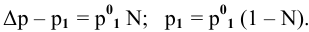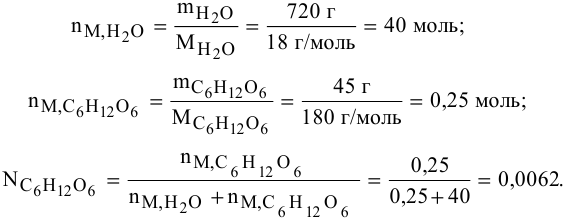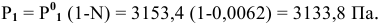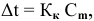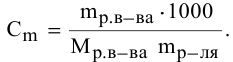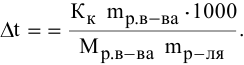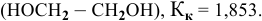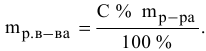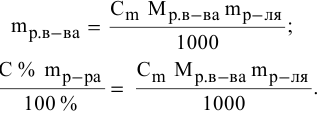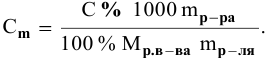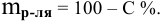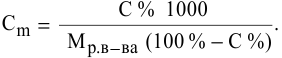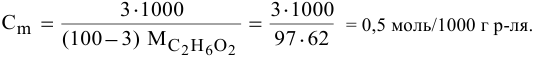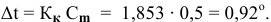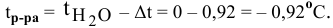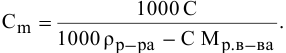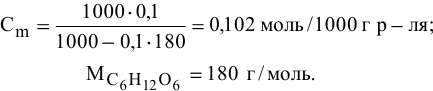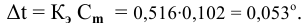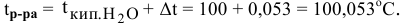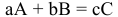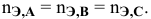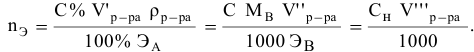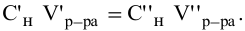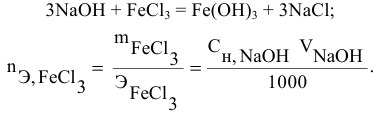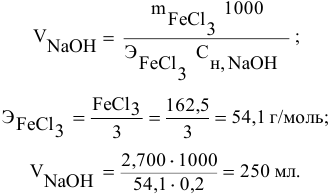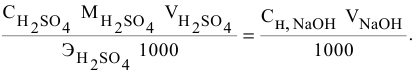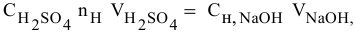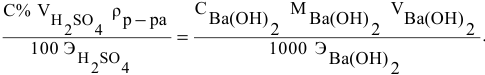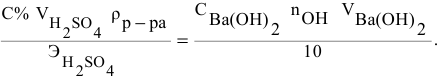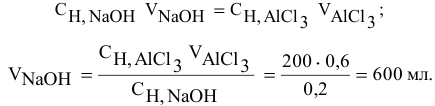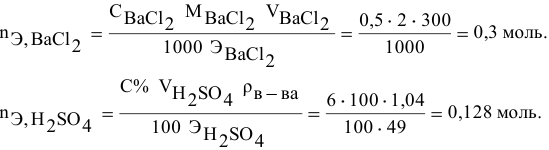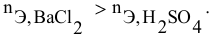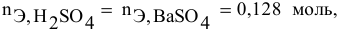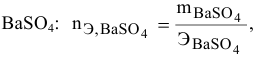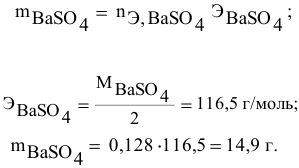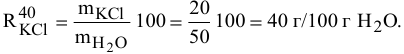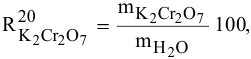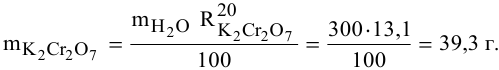Как приготовить раствор химия задачи

Решение задач на растворы

Цели урока: Рассмотреть алгоритм решения задач на растворы: познакомиться с приемами решения задач в математике и химии, рассмотреть биологическое значение воды как универсального растворителя, развить практические умения решать задачи, расширить знания учащихся о значении этих веществ в природе и деятельности человека, сформировать целостную картину о взаимосвязи предметов в школе.

Ход урока

Организационный момент

Учитель математики: Здравствуйте! Сегодня мы проводим необычный урок – урок на перекрестке наук математики и химии.

Учитель химии: Здравствуйте, ребята! Мы с вами увидим, как математические методы решения задач помогают при решении задач по химии.

А чтобы сформулировать тему урока, давайте проделаем небольшой эксперимент.

(Наливаю в 2 хим. стакана воду, добавляю в оба одинаковое количество сульфата меди.) Что получилось? (Растворы). Из чего состоит раствор? (Из растворителя и растворённого вещества). А теперь добавим в один из стаканов ещё немного сульфата меди. Что стало с окраской раствора? (Он стал более насыщенным). Следовательно, чем отличаются эти растворы? (Массовой долей вещ-ва).

Учитель математики: А с математической точки зрения – разное процентное содержание вещества.

Итак, тема урока “Решение задач на растворы”.

Цель урока: Рассмотреть алгоритм решения задач на растворы, познакомить с приемами решения задач в математике и химии, расширить знания о значении этих растворов в быту, сформировать целостную картину о взаимосвязи предметов в школе.

Девиз: “Только из союза двух работающих вместе и при помощи друг друга рождаются великие вещи” Антуан де Сент-Экзюпери.

Учитель математики: Для урока необходимо повторить понятие процента.

– Что называют процентом? (1/100 часть числа).

– Выразите в виде десятичной дроби 17%, 40%, 6%.

– Выразите в виде обыкновенной дроби 25%, 30%, 7%.

40%	1/4
25%	0,04
80%	0,4
4%	4/5

Одним из основных действий с процентами – нахождение % от числа.

Как найти % от числа? (% записать в виде дроби, умножить число на эту дробь.)

– Найти 10% от 30 (10%=0,1 30·0,1=3).

1) 20% от 70;
2) 6% от 20;
3) х% от 7.

– Что такое раствор? (Однородная система, состоящая из частиц растворенного вещества, растворителя и продуктов их взаимодействия.)

– Приведите примеры растворов, с которыми вы встречаетесь в повседневной жизни. (уксус, нашатырный спирт, раствор марганцовки, перекись водорода и др.)

– Какое вещество чаще всего используется в качестве растворителя? (Вода)

Часто понятие “раствор” мы связываем, прежде всего, с водой, с водными растворами. Есть и другие растворы: например спиртовые раствор йода, одеколона, лекарственные настойки.

Хотя именно вода является самым распространённым соединением и “растворителем” в природе.

3/4 поверхности Земли покрыто водой.

Человек на 70% состоит из воды.

В сутки человек выделяет 3 литра воды и столько же нужно ввести в организм.

Овощи – 90% воды содержат (рекордсмены — огурцы — 98%)
Рыба 80% (рекордсмен у животных – медуза 98%)
Хлеб – 40%
Молоко – 75%

– Что такое массовая доля растворенного вещества? (Отношение массы растворенного вещества к общей массе раствора.)

– Вспомните формулу для вычисления массовой доли растворенного вещества и производные от нее (w = m (р.в.)/m (р-ра ) ; m (р.в.)= m (р-ра) · w ; m (р-ра) = m (р.в.)/ w )

– По какой формуле можно рассчитать массу раствора? (m(р-ра) = m (р.в.) + m (р-ля)).

Учитель химии предлагает решить учащимся задачу:

Задача №1. Перед посадкой семена томатов дезинфицируют 15%-ным раствором марганцовки. Сколько г марганцовки потребуется для приготовления 500 г такого раствора? (Ответ: 40 г.)

– Давайте посмотрим на эту задачу с точки зрения математики. Какое правило на проценты вы применили при решении этой задачи? (Правило нахождения процента от числа.)

500·0,15=75 (г) – марганцовки.

– Как видите, задачи, которые вы встречаете на химии, можно решать на уроках математики без применения химических формул.

Задачам на растворы в школьной программе уделяется очень мало времени, но эти задачи встречаются на экзаменах в 9 и 11 классах. В этом году на экзамене в 9 классе была задача на смешивание растворов, и она оценивалась в 6 баллов.

Задача №2. При смешивании 10%-го и 30%-го раствора марганцовки получают 200 г 16%-го раствора марганцовки. Сколько граммов каждого раствора взяли?

Можно ли решить эту задачу так быстро?

О чем говорится в этой задаче? (о растворах)

Что происходит с растворами? (смешивают)

1 раствор
2 раствор

10% = 0,1
30% = 0,3

0,1х
0,3(200-х)

0,16 · 200

Раствор	%-е содержание	Масса раствора (г)	Масса вещества (г)

0,1х + 0,3(200-х) = 0,16 · 200
0,1х + 60 – 0,3х = 32
-0,2х = -28
х = 140
140 (г) – 10% раствора
200 – 140 = 60 (г) — 30% раствора.

Ответ: 140 г, 60 г.

Учитель математики. Рассмотрим еще один раствор – это уксусная кислота. Водный раствор уксусной кислоты, полученный из вина (5-8%) называют винным уксусом. Разбавленный (6-10%) раствор уксусной кислоты под названием “столовый уксус” используется для приготовления майонеза, маринадов и т.д. Уксусная эссенция 80% раствор. Ее нельзя применять без разбавления для приготовления пищевых продуктов. “Столовый уксус”, используют для приготовления маринадов, майонеза, салатов и других пищевых продуктов. Очень часто при приготовлении блюд под руками оказывается уксусная эссенция. Как из нее получить столовый уксус. Поможет следующая задача.

Задача №3. Какое количество воды и 80%-го раствора уксусной кислоты следует взять для того, чтобы приготовить 200 г столового уксуса (8%-ый раствор уксусной кислоты.)

%-е содержание

Масса раствора (г)

Масса вещества (г)

Уксусная кислота
Вода

0,08 · 200

0,8х = 0,08 · 200
0,8х = 16
х = 16 : 0,8
х = 20
20 (г) – уксусной кислоты
200 – 20 = 180 (г) – воды.

Ответ: 20 г, 180 г.

Учитель химии. А сейчас мы решим экспериментальную задачу.

Приготовить 20 г 5%-го раствора поваренной соли. (Расчётная часть). Затем выполняем практическую часть. (Напомнить правила Т-Б).

2. Экспериментальная часть (Соблюдать правила техники безопасности).

1. Уравновесить весы.
2. Взвесить необходимое количество соли.
3. Отмерить мерным цилиндром воду.
4. Смешать воду и соль в стакане.

Учитель математики. Проведем проверочную работу, в которую включили задачи из сборника для подготовке к экзаменам в 9-м классе.

Проверочная работа

При смешивании 15%-го и 8% -го раствора кислоты получают 70 г 10%-го раствора кислоты. Сколько граммов каждого раствора взяли?	При смешивании 15%-го и 60% -го раствора соли получают 90 г 40%-го раствора соли. Сколько граммов каждого раствора взяли?
1р 15% = 0,15 х 0,15х	1р 15%=0,15 х 0,15х
2р 8% = 0,08 70 — х 0,08(70 — х)	2р 60% = 0,6 90 — х 0,6(90 — х)
см 10% = 0,1 70 0,1 · 70	3р 40% = 0,4 90 0,4 · 90
0,15х + 0,08(70 — х) = 0,1 · 70 0,15х + 5,6 — 0,08х = 7 0,07х = 7 — 5,6 0,07х = 1,4 х = 1,4:0,07 х = 20 20(г) – 15%-го раствора. 70 – 20 = 50 (г) — 8% раствора Ответ: 20 гр., 50 г.	0,15х + 0,6(90 — х) = 0,4 · 90 0,15х + 54 — 0,6х = 36 -0,45х = 36 — 54 -0,45х =-18 х = 18 : 0,45 х = 40 40 (г) -15% раствора. 90 — 40 = 50 (г) — 60% раствора. Ответ: 40 гр., 50 г.

Подведение итогов урока

– Посмотрите на содержание всех решенных сегодня задач. Что их объединяет? (Задачи на растворы.)

– Действительно, во всех задачах фигурируют водные растворы; расчеты связаны с массовой долей растворенного вещества; и если вы обратили внимание, задачи касаются разных сторон нашего быта.

– Посмотрите на эти задачи с точки зрения математики. Что их объединяет? (Задачи на проценты.)

При решении всех этих задач мы используем правило нахождения процента от числа.

Оценки за урок.

Домашнее задание.

Важное место в рационе питания человека, а особенно детей занимает молоко и молочные продукты. Решим такую задачу:

Задача №1. Какую массу молока 10%-й жирности и пломбира 30%-й жирности необходимо взять для приготовления 100 г 20%-го новогоднего коктейля?

%-е содержание

Масса раствора (г)

Масса вещества (г)

Молоко
Пломбир

10% = 0,1
30% = 0,3

х
100 — х

0,1х
0,3(100 — х)

Коктейль

0,1х + 0,3(100-х) = 0,2 · 100
0,1х + 30 – 0,3х = 20
-0,2х = -10
х = 50
50(г) – молока
100 – 50 = 50(г) – пломбира.
Ответ:50 г молока, 50 г пломбира.

Задача №3. Для засола огурцов используют 7% водный раствор поваренной соли (хлорида натрия NaCl). Именно такой раствор в достаточной мере подавляет жизнедеятельность болезнетворных микроорганизмов и плесневого грибка, и в то же время не препятствует процессам молочнокислого брожения. Рассчитайте массу соли и массу воды для приготовления 1 кг такого раствора?

Раствор
Разбавленный, водный
Растворять, смешивать, решать
Растворы широко встречаются в быту.
Смеси

Наш урок подошел к концу. Сейчас каждый из вас оставит на парте тот смайлик, какое настроение вы приобрели на уроке.

Источник

Задачи с решениями на концентрацию растворов

Концентрация растворов. Растворы неэлектролитов. Растворимость

Задача:

Расчеты по процентной концентрации растворов. Формула, выражающая процентную концентрацию раствора —

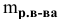
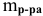
где — масса растворенного вещества;

— масса раствора,

Задача:

Рассчитать процентную концентрацию раствора, полученного растворением 80 г сахара в 160 г воды.

Решение:

Задача:

Рассчитать массы поваренной соли и воды, необходимые для приготовления 250 г 2,5%-ного раствора.

Решение:

Задача:

Рассчитать концентрацию раствора, полученного смешением З00 г 10%-ного раствора хлороводорода и 400г 20%-ного раствора хлороводорода.

Решение:

Определяем массы растворенной 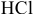в каждом растворе:

Определяем концентрацию полученного раствора:

Задача:

Какова концентрация серной кислоты в растворе, полученном смешиванием 200г 10%-ного раствора серной кислоты и 100г 5%-ного раствора сульфата натрия?

Решение:

Масса полученного раствора определяется как сумма масс смешанных растворов:

Далее определим концентрацию серной кислоты в полученном растворе:

Задача:

Расчеты по молярной концентрации (молярности) раствора.

Формула для расчета молярности раствора —

где С — молярность раствора, моль/л;

— масса растворенного вещества, г;

— молярная масса растворенного вещества, г/моль;

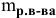
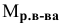
V — объем раствора, мл; если объем выражается в литрах, тогда в формуле исчезает коэффициент 1000.

Задача:

Какая масса серной кислоты необходима для приготовления 2 л 2-молярного раствора?

Решение:

Задача:

250 мл раствора содержат 7г КОН. Какова молярность этого раствора?

Решение:

Задача:

Расчеты по нормальной концентрации (нормальности) раствора.

Для расчета нормальности пользуемся следующей формулой:

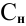
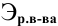
где — нормальная концентрация раствора;

— эквивалентная масса растворенного вещества.

Задача:

Какая масса фосфорной кислоты необходима для приготовления 2 л 0,1 н раствора?

Решение:

Задача:

Расчеты по разбавлению растворов.

Выведем формулу для расчетов при разбавлении растворов, учитывая, что концентрация как исходного, так и приготовленного растворов может быть выражена любым способом 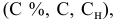, а также исходя из того, что при разбавлении растворов постоянной остается масса растворенного вещества.

Для раствора, концентрация которого выражена в процентах,

а так как

где 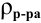— плотность раствора, г/мл.

Для молярной концентрации

Для нормальной концентрации

Приравниваем правые части уравнений:

Задача:

Сколько миллилитров 98%-ного раствора серной кислоты

( = 1,84 г/мл) необходимо для приготовления 300 мл 3 н раствора этой кислоты?

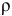
Решение:

Воспользуемся первым членом приведенного выше уравнения для концентрированного исходного раствора кислоты и третьим членом — для приготовления разбавленного раствора серной кислоты:

= 3 экв/л;

— неизвестный объем исходного раствора;

= 300 мл;

= 49 г/моль.

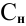
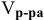
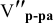
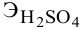
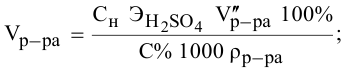
Задача:

Расчеты по переходу от одного способа выражения концентрации данного раствора к другому.

При переходе от одной концентрации данного раствора к другой остаются постоянными не только масса растворенного вещества, но и объем раствора, т.е.

Предыдущая формула принимает следующий вид:

Задача:

Определить молярность 36,5%-ного раствора соляной кислоты (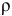=1,18 г/мл).

Решение:

Воспользуется первым и вторым членами последнего уравнения и выведем выражение для определения молярности:

Задача:

Расчеты по законам Рауля. Давление паров разбавленного раствора.

По закону Рауля, понижение давления пара 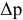над раствором прямо пропорционально мольной доле растворенного вещества:

где 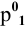— давление пара чистого растворителя;

N — мольная доля растворенного вещества,

где 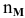— число молей растворенного вещества и растворителя.

где 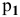— давление паров растворителя над раствором.

Задача:

Определить давление насыщенных паров раствора, содержащего 45 г глюкозы 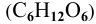в 720 г воды при 25°С. Давление насыщенного пара воды при 25°С равно 3153,4 Па.

Решение:

Рассчитываем мольную долю растворенного вещества:

Определяем давление паров воды над раствором:

Задача:

Расчеты по понижению температуры замерзания растворов.

По закону Рауля понижение температуры замерзания прямо пропорционально моляльной концентрации раствора:

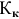
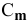
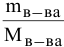
где — криоскопическая постоянная растворителя;
— моляльная концентрация раствора (число молей растворенного вещества в 1000 г растворителя),

Задача:

Рассчитать температуру замерзания 3%-ного водного раствора этиленгликоля

Решение:

Выведем формулу для перехода от процентной концентрации к моляльности раствора.

Для процентной концентрации

Если принять 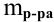за 100, тогда

Находим моляльность рассматриваемого раствора:

Рассчитаем понижение температуры замерзания раствора:

Температура замерзания водного раствора

Задача:

Рассчитать температуру кипения 0,1 молярного водного раствора глюкозы ( 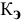= 0,516).

Решение:

Формула для перехода от молярной концентрации к моляльной —

Так как раствор разбавленный, то принимаем 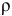= 1 г/мл, тогда

Определяем повышение температуры кипения раствора:

Температура кипения этого раствора

Задача:

Расчеты по уравнению химической реакции, протекающей в растворе.

Для химического уравнения общего вида

верно следующее соотношение числа эквивалентов:

Если участвующие в реакции вещества взяты в виде растворов и если их концентрации выражены:

а) для вещества А — С %;

б) для вещества В — С (молярность);

в) для вещества С — 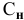(нормальность),

тогда массы и число эквивалентов каждого из веществ, находящихся в определенных объемах растворов этих веществ, определяются по формулам:

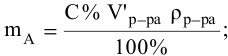
Так как числа эквивалентов, участвующих в реакции веществ, равны между собой, то можно записать:

Если концентрации участвующих в реакции веществ выражены в нормальности, то формула для расчетов приобретает вид:

Задача:

Какой объем 0,2 н раствора щелочи необходим для осаждения 2,708 г хлорида трехвалентного железа в виде гидроксида железа?

Решение:

Предложенный метод не требует обязательного написания уравнения реакции для осуществления таких расчетов.

Задача:

Для нейтрализации 20 мл 2-молярного раствора 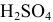необходимо 8 мл раствора щелочи. Какова нормальность щелочи ?

Решение:

Формула для расчета —

Так как — числу атомов водорода, участвующих в реакции, то формула примет вид

Задача:

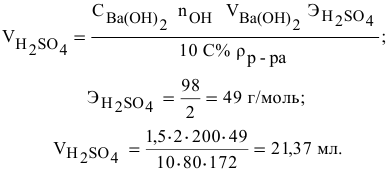
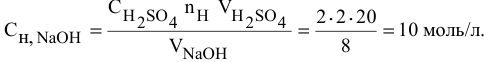
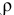
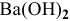
Какой объем 80 %-ного раствора ( = 1,72 г/мл) необходим для реакции с 200 мл 1,5-молярного раствора ?

Решение:

Формула для расчета —

Так как 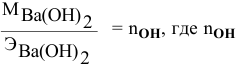— число групп ОН, участвующих в реакции, то

Задача:

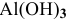
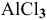
Какой объем 0,2 н раствора щелочи необходим для реакции осаждения с 200 мл 0,6 н раствора ?

Решение:

Формула для расчета —

Задача:

Смешивается 300 мл 0,5 М раствора хлорида бария со 100 мл 6 %-ного раствора серной кислоты ( 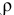= 1,04 г/мл). Какова масса полученного осадка?

Решение:

, полученный осадок — сульфат бария.

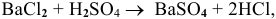
Так как указаны количества обоих реагирующих веществ, то необходимо определить вещество, взятое в избытке.

Таким образом, 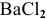взято в избытке:

Дальнейший расчет производим по веществу, взятому в недостатке, т.е. по серной кислоте.

Так как

находим массу

Задача:

Для приготовления насыщенного раствора К.С1 при 40°С взято 50г воды и 20г КС1. Какова растворимость К.С1 в воде при данной температуре?

Решение:

Задача:

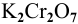
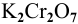
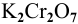
В 300г горячей воды растворено 219г . Найти массу кристаллов , полученных при охлаждении приготовленного горячего раствора до 20°С. Известно, что растворимость при 20°С равна 13,1 г на 100 г воды.

Решение:

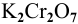
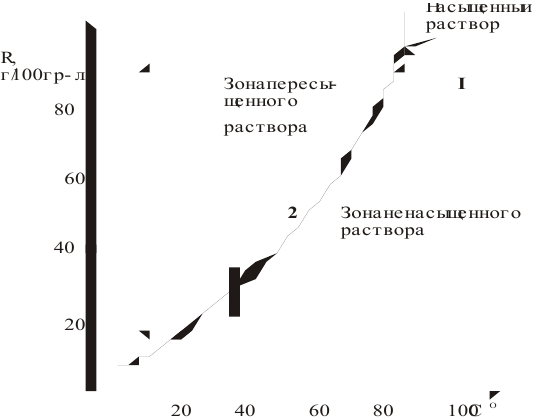
Определяем, сколько может быть растворено в 300 г воды при 20°С:

Масса кристаллов — это разность массы растворенного вещества в горячем растворе и массы растворенного вещества в охлажденном растворе (рис.З):

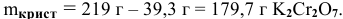
Рис. 3 — Графическое изображение процесса выпадения кристаллов при охлаждении раствора:

1 — участок охлаждения ненасыщенного раствора от заданной температуры до температуры образования насыщенного раствора;

2 — участок охлаждения насыщенного раствора до заданной температуры с уменьшением растворимости вещества, что приводит к его кристаллизации (в данном случае мы предполагаем, что пересыщенный раствор не образуется).

Эти задачи взяты со страницы решения задач по неорганической химии:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник